机器学习16--增强学习——有限状态的马尔科夫决策过程MDP
文章目录
机器学习16—增强学习——有限状态的马尔科夫决策过程MDP
16-20讲均为增强学习相关知识。暂时,只对16、17进行总结。
增强学习:找到一条回报值最大的路径(每步的回报之和最大),就认为是最佳的路径。eg:四足机器人、象棋 AI 程序、机器人控制,手机网络路由,市场决策,工业控制,高效网页索引等。
马尔科夫决策过程——MDP
基本概念
- 一个马尔科夫决策过程由一个五元组构成
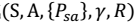

- 概念:
- 值函数:
为了区分不同π的好坏,并定义在当前状态下,执行某个策略π后,出现的结果的好坏, 需要定义值函数: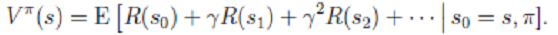
- 策略(pllicy):

公式推导(最优值函数和最优策略)
- 对于如下问题,Robot开始位于(3,1)位置。目的是右上角。可能有11个状态。
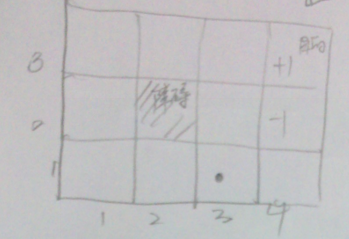
- 行走的概率:
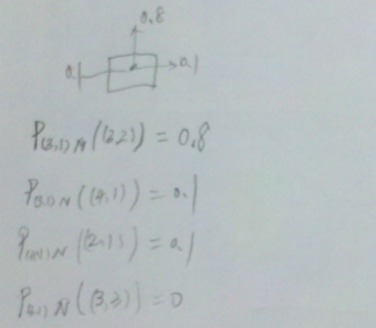
- 回报函数
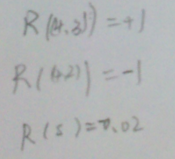
- 在某一点时的值函数。对于上述问题,有11个方程,11个未知量。

- 行走的概率:
- 进一步化简,我们得到
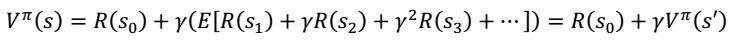
Bellman 等式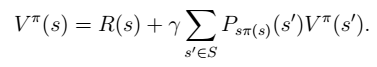
其中,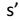 表示下一个状态。
表示下一个状态。 - 定义最优值函数:$V^{\star}$。从而,找到一个当前状态 s 下,最优的行动策略π。
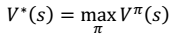
- 最终,我们得到想要的最优值函数和最优策略:
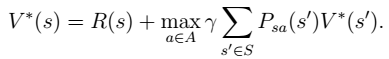
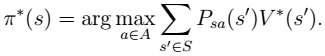
- 这里需要注意的是,如果我们能够求得每个 s 下最优的 a,那么从全局来看,
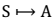 的
的
映射即可生成,而生成的这个映射是最优映射,称为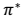 。
。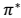 针对全局的 s,确定了每一个 s的下一个行动 a,不会因为初始状态 s 选取的不同而不同。
针对全局的 s,确定了每一个 s的下一个行动 a,不会因为初始状态 s 选取的不同而不同。
有限状态的MDP具体策略的有效算法——值迭代和策略迭代法
前提:状态有限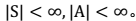
值迭代法
- 过程
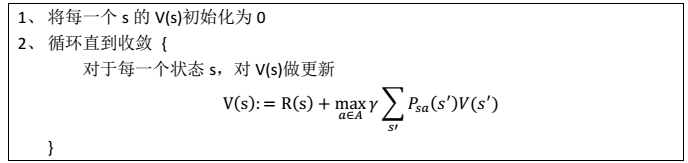
其中,迭代公式也可以写作: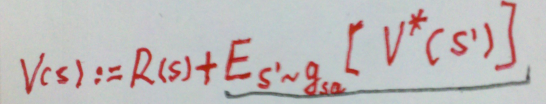
- 内循环的有两种策略:

- 两种迭代法最终收敛到$V^{\star}$。我们再用如下公式,求出最优策略$\pi^{\star}$
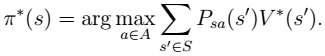
策略迭代法


注:在1-(a)中,我们认为得到的V为最优值函数。然后,在(b)中,进行更新得到最优策略。一直重复,知道得到真正的最优策略$\pi^{\star}$。
- (a)步中的 V 可以通过之前的 Bellman 等式求得
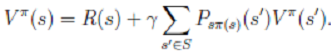
(b)步实际上就是根据(a)步的结果挑选出当前状态 s 下,最优的 a,然后对π(s)做更新。这里的两个步骤,相当于求解11(状态个数)个线性方程。如果状态非常多,显然计算量相当大。
两种方法的总结
规模比较小的 MDP: 策略一般能够更快地收敛。
规模很大(状态很多)MDP:值迭代比较容易(不用求线性方程组)。
MDP 中的参数估计
实际中:
- 未知量:状态转移概率$P_{sa}$𣠠和回报函数 R(s)
- 已知量: S、 A 和γ
下面我们对状态转移概率$P_{sa}$和回报函数 R(s)进行估计:
- 假设我们已知很多条状态转移路径如下:(相当于样本)
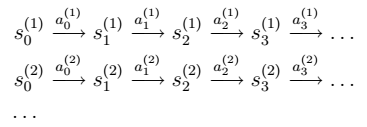
其中:
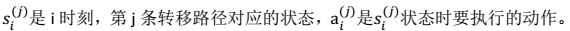
- 如果我们获得了很多上面类似的转移链(相当于有了样本),那么我们就可以使用最大似然估计来估计状态转移概率。
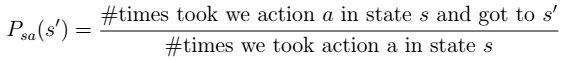
注:分子是从 s 状态执行动作 a 后到达 s’的次数,分母是在状态 s 时,执行 a 的次数。两者相除就是在 s 状态下执行 a 后,会转移到 s’的概率。
- 同样,如果回报函数未知,那么我们认为 R(s)为在 s 状态下已经观测到的回报均值。
- 我们将参数估计和值迭代结合起来(在不知道状态转移概率情况下)的流程如下:

在(b)步中我们要做值更新,也是一个循环迭代的过程,在上节中,我们通过将 V 初始化为 0,然后进行迭代来求解 V。嵌套到上面的过程后,如果每次初始化 V 为 0,然后迭代更新, 就会很慢。一个加快速度的方法是每次将 V 初始化为上一次大循环中得到的 V。 也就是说 V 的初值衔接了上次的结果。
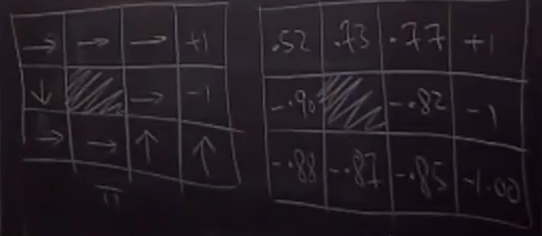
NG老师的黑板图
最后把两张NG老师画的图放过来