机器学习15-3--独立成分分析ICA(Independent Component Analysis)
文章目录
机器学习15-3—独立成分分析ICA(Independent Component Analysis)
- 每个人发出的信号$s$独立。且信号不能是高斯分布。
- 用于信号的分离(鸡尾酒宴会问题)。
ICA问题
鸡尾酒宴会问题
- n个人,n个麦克风。从n个麦克风得到一组数据:
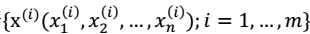 。其中:i 表示采样的时间顺序,也就是说共得到了 m 组采样,每一组采样都是 n 维的。
。其中:i 表示采样的时间顺序,也就是说共得到了 m 组采样,每一组采样都是 n 维的。 - 我们的目标是单单从这 m 组采样数据中分辨出每个人说话的信号s。有 n 个信号源
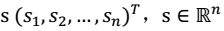 ,s相互独立。
,s相互独立。 - A 是一个未知的混合矩阵(mixing matrix),用来组合叠加信号 s。
- 我们可以得到:
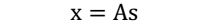
其中, x 不是一个向量,是一个矩阵
- 其中每个列向量

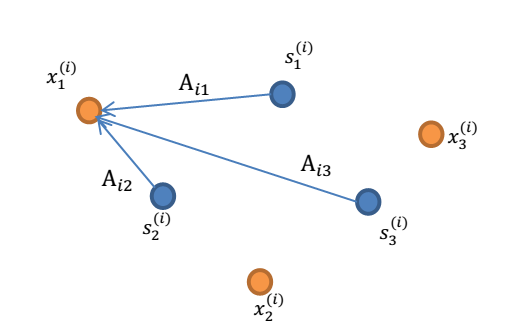
- A 和 s 都是未知的,x 是已知的,我们要想办法根据 x 来推出 s。这个过程也称作为盲信号分离。
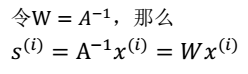
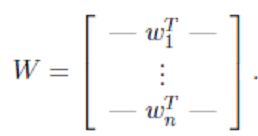
- 最终得到:
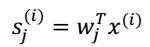
- $s_{(i)}^{j}$:表示speaker j 在时刻i发出的信号。
- 对于此,我们需要知道两个量才能求出另外一个,下面我们进一步分析。
ICA算法的前处理步骤
- 中心化:也就是求 x 均值,然后让所有 x 减去均值,这一步与 PCA 一致。
- 漂白:目的是为了让x相互独立。将 x 乘以一个矩阵变成
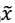 (其协方差矩阵是$I$)。
(其协方差矩阵是$I$)。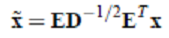
- 其中,
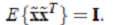
- 其中使用特征值分解来得到 E(特征向量矩阵)和 D(特征值对角矩阵) ,计算公式为
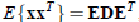
- 其中,
ICA算法
- 我们假定每$s_i$有概率密度$p_s$,那么给定时刻原信号的联合分布就是
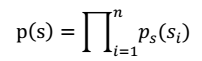
注:每个人发出的声音信号s各自独立。
- 然后,我们就可以求得p(x)
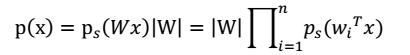
- 现在,我们需要知道p(s)和w,才能求得p(x)。
首先,我们假设s 的累积分布函数符合 sigmoid 函数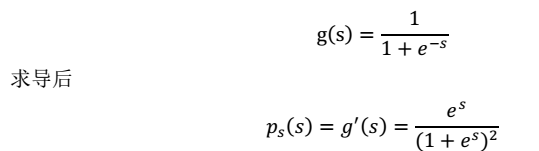
这就是 s 的密度函数。这里 s 是实数。 然后,我们就剩下W了。我们用最大似然估计的方法求解。
使用前面得到的 x 的概率密度函数,得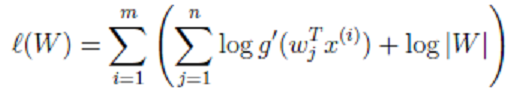

最终,我们求得: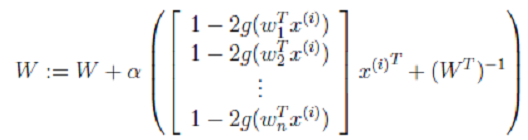
其中α是梯度上升速率,人为指定。
迭代求出 W 后,我们也可以还原出原始信号:
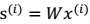
应用
如果把麦克风x换成采集脑电波的电极,信号源s就代表大脑独立进程:心跳、眨眼等。通过将信号x减去心跳、眨眼等无用信号,我们就可以得到大脑内部信号。
小结
- ICA 的盲信号分析领域的一个强有力方法,也是求非高斯分布数据隐含因子的方法。
- ICA和PCA对比:
- ICA: 从之前我们熟悉的样本-特征角度看,我们使用 ICA 的前提条件是,认为样本数据由独立非高斯分布的隐含因子产生,隐含因子个数等于特征数。更适合用来还原信号(因为信号比较有规律,经常不是高斯分布的)。
- PCA : 认为特征是由 k 个正交的特征(也可看作是隐含因子)生成的。更适合用来降维(用那么多特征干嘛,k 个正交的即可)
- 有时候也需要组合两者一起使用。

