机器学习14—PCA主成分分析

概述

• 高斯分布的样本
• 原始变量的线性组合表示新的综合变量，即主成分
• 解决特征过多，样本过少的问题
• 两个特征强相关的问题，或者两个特征有一个多余
• 滤除噪声
• 与《模型选择和规则化》对比

  《模型选择和规则化》要剔除的特征主要是和类标签无关的特征。比如“学生的名字”就和他的“成绩”无关，使用的是互信息的方法。
  而这里的特征很多是和类标签有关的，但里面存在噪声或者冗余。在这种情况下，需要一种特征降维的方法来减少特征数，减少噪音和冗余，减少过度拟合的可能性。

• PCA的思想是将n维特征映射到k维上（k<n），这k维是全新的正交特征。这k维特征称为主元，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n‐k维特征。

PCA过程

1. 数据预处理：减去均值，再归一化(除以标准差)。
   

   

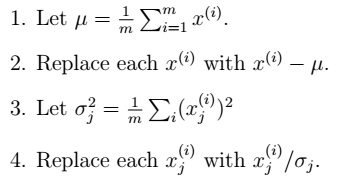
2. 求特征协方差矩阵，如果数据是3维，那么协方差矩阵是
   
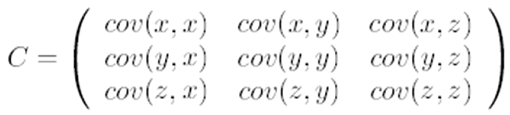
3. 求协方差的特征值和特征向量
4. 将特征值按照从大到小的顺序排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。

   这里，用简单的方式理解一下为什么选取前k个：在矩阵特征值与特征向量中，越大的特征值对应的特征向量，对被变换矩阵影响越大。

5. 将样本点投影到选取的特征向量上。假设样例数为m，特征数为n，减去均值后的样本矩阵为$DataAdjust(mn)$，协方差矩阵是 $nn$，选取的k个特征向量组成的矩阵为$EigenVectors(n*k)$。那么投影后的数据FinalData为
   

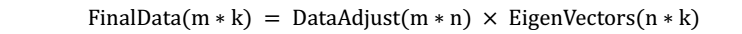
PCA 理论基础

为什么协方差矩阵的特征向量就是k维理想特征，有三个理论：分别是最大方差理论、最小错误理论和坐标轴相关度理论。详见课件。

最大方差理论

简单理解一下第一种方法：
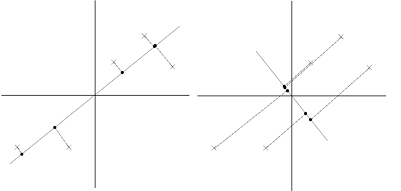
在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。如前面的图，样本在横轴上的投影方差较大，在纵轴上的投影方差较小，那么认为纵轴上的投影是由噪声引起的。
因此我们认为，最好的k维特征是将n维样本点转换为k维后，每一维上的样本方差都很大。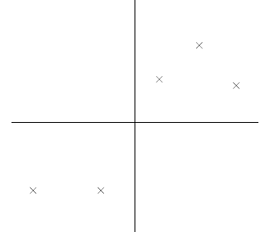

1. 方差：
   
   
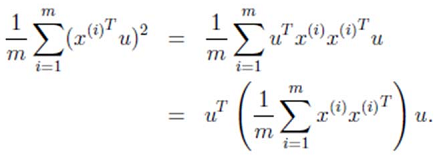
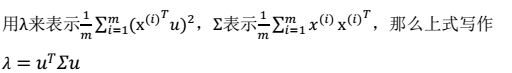
2. 求解最值问题：
   
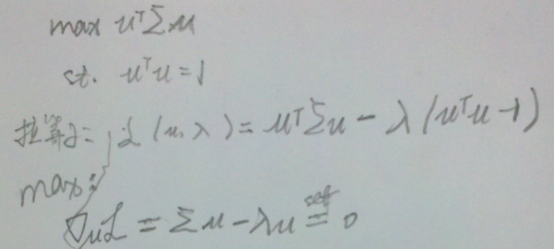
3. 最终解：
   

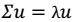
   λ就是Σ的特征值，u是特征向量。最佳的投影直线是特征值λ最大时对应的特征向量，其次是λ第二大对应的特征向量，依次类推。
   
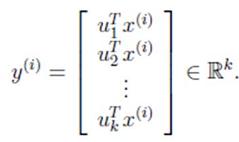
   其中的第j 维就是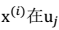 上的投影。
   通过选取最大的k个u，使得方差较小的特征（如噪声）被丢弃。