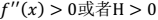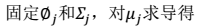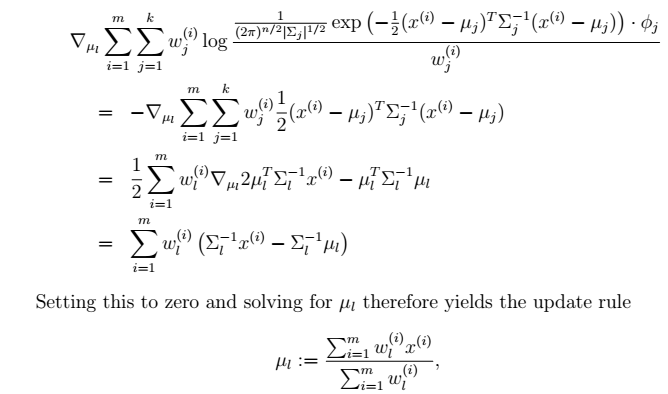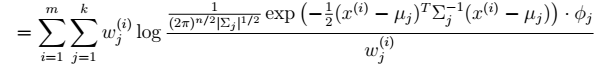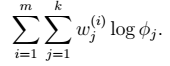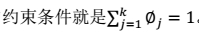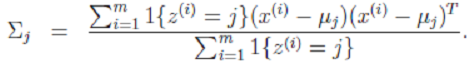机器学习12-2--EM算法--应用到三个模型: 高斯混合模型 ,混合朴素贝叶斯模型,因子分析模型(下一部分)
机器学习12-2—EM算法—应用到三个模型: 高斯混合模型 ,混合朴素贝叶斯模型,因子分析模型(下一部分)
- 判别模型求的是条件概率p(y|x)。常见的判别模型有线性回归、对数回归、线性判别分析、支持向量机、boosting、条件随机场、神经网络等。
- 生成模型求的是联合概率p(x,y),即 = p(x|y) ∗ p(y) 。常见的生成模型有隐马尔科夫模型、朴素贝叶斯模型、高斯混合模型、LDA、Restricted Boltzmann Machine等。
所以这里说的高斯混合模型,混合朴素贝叶斯模型都是求p(x,y)联合概率的。(下面推导会见原因)
总结:凡是生成模型,目的都是求出联合概率表达式,然后对联合概率表达式里的各个参数再进行估计,求出其表达式。
下面的EM算法,GMM等三个模型都是做这同一件事:设法求出联合概率,然后对出现的参数进行估计。
EM算法
Jensen不等式
Jensen不等式表述如下:
如果 f 是凸函数,X 是随机变量,那么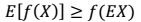
- 凸函数:
- 如果 f 是严格凸函数,那
当且仅当
。即:也就是说 X 是常量(后面会用到这个结论)。𞀊- Jensen 不等式应用于凹函数时,不等号方向反向,也就是
。后面的log函数就是凹函数。
回顾:函数的期望的求取

EM算法推导步骤
- EM算法的作用:进行参数估计。
- 应用:(因为是无监督,所以一般应用在聚类上,也用在HMM参数估计上)所以凡是有EM算法的,一定是无监督学习.因为EM是对参数聚集
- 我们的目的:找到每个样例隐含的类别 z,能使得 p(x,z)最大。(即 如果将样本x(i)看作观察值,隐含类别z看作是隐藏变量, 则x可能是类别z, 那么聚类问题也就是参数估计问题)
p(x,z)最大似然估计是:
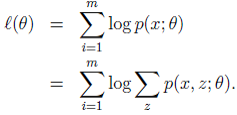
所以可见用EM算法的模型(高斯混合模型,朴素贝叶斯模型)都是求p(x,y)联合概率,为生成模型。 - 对上面公式,直接求θ一般比较困难,因为有隐藏变量z存在,但是一般确定了z后,求解就容易了。
- p(x,z)最大似然估计是:
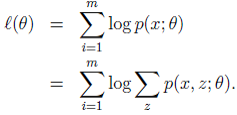
- EM是一种解决存在隐含变量优化问题的有效方法。既然不能直接最大化ℓ(θ),我们可建立ℓ的下界(E步),再优化下界(M步),见下图第三步,取的就是下界
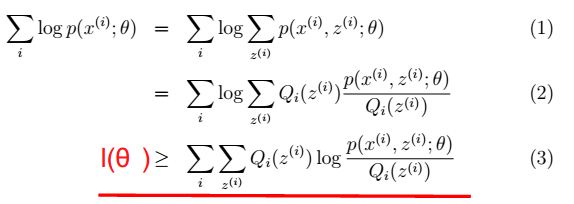
其中,
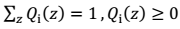
如果 z 是连续性的,那么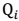 是概率密度函数,需要将求和符号换做积分符号(因子分析模型是如此),即:
是概率密度函数,需要将求和符号换做积分符号(因子分析模型是如此),即: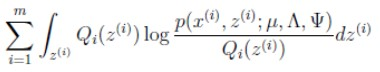
- 对Q(z)进行推导:
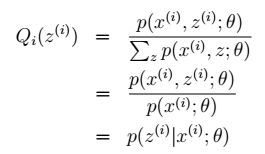
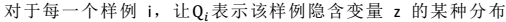
- z只受参数θ影响:
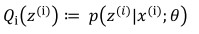
一般的EM算法步骤
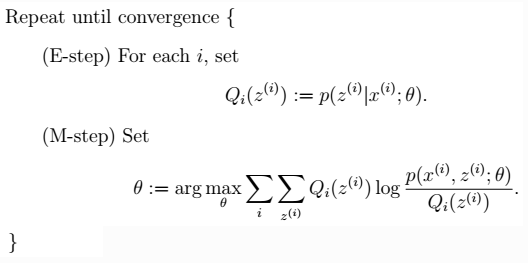
- 注:在m步中,最终是对参数θ进行估计,而这一步具体到高斯混合模型,则θ有三个参数:$\mu,\phi, \sigma$ 代替,即高斯混合模型要推导三个参数,下面会讲。
- 最终,我们得到的是每个样例属于哪个类(k个类),以及参数θ(k组)。
至此,这就是EM算法所有推导,EM算法推导也只能推导这些步,具体再将这些公式推导下去,就要结合模型了。
EM算法的另外一种解释——坐标上升算法
如果我们定义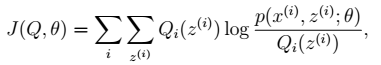
从前面的推导中我们知道ℓ(θ) ≥ J(Q, θ),EM 可以看作是 J 的坐标上升法,E 步固定θ,优化Q;M 步固定Q优化θ。
EM算法的图形解释
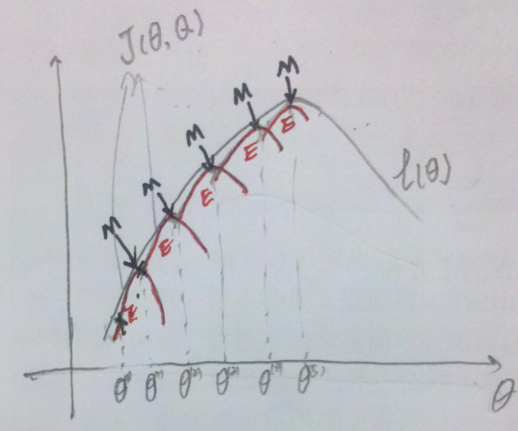
其中,红色线表示每一步的J(Q, θ)。E步:确定红线部分。M步:确定当前红线部分J(Q, θ)的极值点。最终得到局部最优解。
混合高斯模型
将EM算法融到高斯混合模型,将上面EM算法的E步、M步的公式再具体推导下去。
混合高斯模型定义:对于每个样例$x^{(i)}$ ,我们先从k个类别中按多项式分布抽取一个$z^{(i)}$(隐含随机变量) ,然后根据所对应的 k 个多值高斯分布中的一个,生成样例$x^{(i)}$,整个过程称作混合高斯模型。
条件和符号说明
- 训练样本:
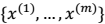
- $x^{(i)}$ :满足多值高斯分布,即:
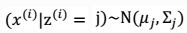 。由此可以得到联合分布:
。由此可以得到联合分布: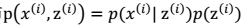 。
。 - 隐含类别:
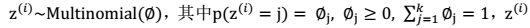 有 k 个值{1,…,k} 可以选取。
有 k 个值{1,…,k} 可以选取。
混合高斯模型步骤
E步
1、由EM公式得
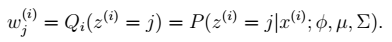
M步
2、我们需要在固定 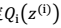 后最大化最大似然估计,求解
后最大化最大似然估计,求解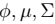
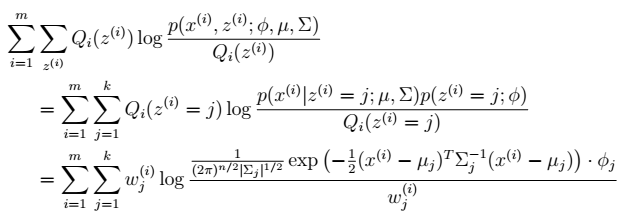
3、 求解三个参数
在∅和μ确定后,分子上面的一串都是常数了,实际上需要优化的公式是:
显然这是一个,有约束条件的规划问题。我们采用前面的拉格朗日方法:- Σ的推导也类似,不过稍微复杂一些,毕竟是矩阵。
4、混合高斯模型与前面的高斯判别模型的对比
- 最大似然估计就近似于高斯判别分析模型
- GDA 中类别 y 是伯努利分布,而这里的 z是多项式分布
- 这里的每个样例都有不同的协方差矩阵,而 GDA 中认为只有一个。
5、总结:
最终,我们得到隐含类别的具体值。还有,参数∅μΣ。
混合朴素贝叶斯模型
混合高斯的例子:文本聚类: 要对一系列的文本聚类成若干主题。(用svm写文本分类是最好的)news.google.com就是文本聚类一个应用。垃圾邮件过滤(不知道那一封是垃圾邮件)。
模型描述
给定m个样本的训练集合是 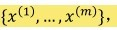 , 每个文本$x^{(i)}$属于$(0,1)^n$。即每个文本是n维 0或1的向量。
, 每个文本$x^{(i)}$属于$(0,1)^n$。即每个文本是n维 0或1的向量。
故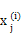 = { wordj 是否出现在文本i 里}
= { wordj 是否出现在文本i 里}
我们要对$z^{i}$(值是0或1) 进行建模,$z^{i}$是隐含随机变量,这里取两个值:2个聚类。所以对混合贝叶斯模型,假设$z^{i}$服从参数∅有伯努利分布。
步骤
1、同高斯混合模型,混合贝叶斯模型的联合概率是: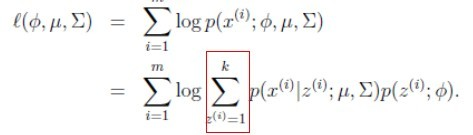
2、由贝叶斯公式可知: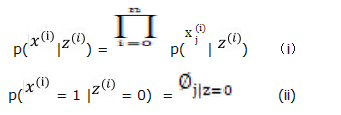
3、E步: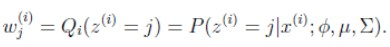
注:这里三个参数phi,mu,sigma,改成,
,
与$∅_{j|z}$
4、M步: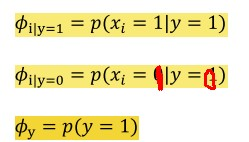
得到: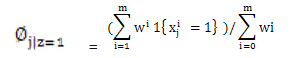
这里Wi表示文本来自于类1,分子Σ表示:类1且包含词j的文档个数,分布表示类1的文档总数。所以全式表示:类1包含词j的比率。
EM算法不能做出绝对的假设0或者1,所以只能用Wi表示,最终Wi的值会靠近0或1,在数值上与0或1无分别。
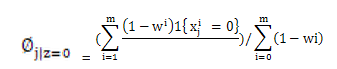
全式表示:类0包含词j的比率
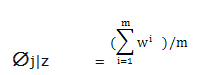
5、迭代上面12步骤,收敛,得到参数估计。然后,带回联合概率,将联合概率排序,由联合概率最高值 ,可得知哪个文本是输入哪个类了。