机器学习12-1--K-means算法(无监督)
机器学习12-1—K-means算法(无监督)
本章开始接触第一个无监督学习算法。无监督学习算法可用在新闻局累、图像分割等。
无监督学习概念
- 定义:简单讲,就是没有分类标签y。非监督式学习是一种机器学习的方式,并不需要人力来输入标签。它是监督式学习和强化学习等策略之外的一种选择。
- K-means是最简单的聚类,聚类属于无监督学习。
K-means的步骤
- 符号:
类的数目:$k$
训练样本: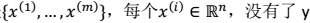
质心点: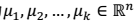
类:${c^{(1)}, c^{(2)}, ……, c^{(k)}}$ - 步骤:
K-means 算法是将样本聚类成 k 个簇(cluster),具体算法描述如下:
- 二维效果图(k=2):
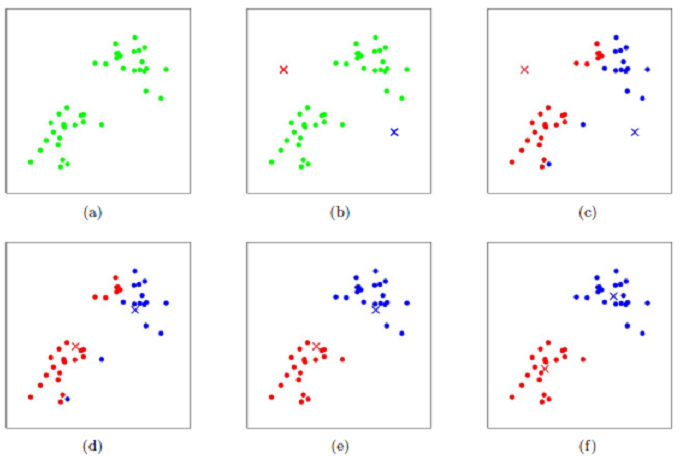
- Kmeans收敛的原因
首先,我们定义畸变函数(distortion function)如下:
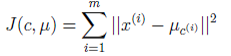

注:由于畸变函数 J 是非凸函数,意味着我们不能保证取得的最小值是全局最小值,也就是说 k-means对质心初始位置的选取比较感冒,但一般情况下k-means达到的局部最优已经满足需求。但如果你怕陷入局部最优,那么可以选取不同的初始值跑多遍 k-means,然后取其中最小的 J 对应的μ和 c 输出。 - 聚类后结果是一个个星团,星团里面的点相互距离比较近,星团间的星星距离就比较远了。
K-means与EM的关系:
EM的基本思想:
- E步:固定参数θ,优化隐含类别Q
- M步:固定隐含类别Q,优化参数θ
K-means用到的EM的基本思想:
- E步:确定隐含类别变量c
- M步:更新其他参数μ来使J最小化
两种算法都类似于坐标上升法。固定一个,优化另外一个。

