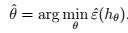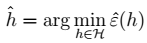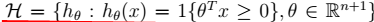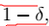机器学习9—学习理论的基础知识

基本符号

• $\epsilon$ 泛化误差：

  • 从训练样本数据中推导的规则，能够适用于新的样本的能力。
  • 对服从分布D的样本，分类错误的概率。

• $\hat{\epsilon}$ 训练误差

  • 训练误差在训练样本中训练出的规则，能够适用于训练样本的能力。
  • 对训练样本，分类错误的部分，在总的训练集中所占比例**。

• $h$
• $\hat{h }$

  • $\theta$ 和 $\hat{\theta }$关系：ERM风险最小化$\theta$的过程：

• $h$和 $\hat{h }$关系：ERM风险最小化$h$的过程：

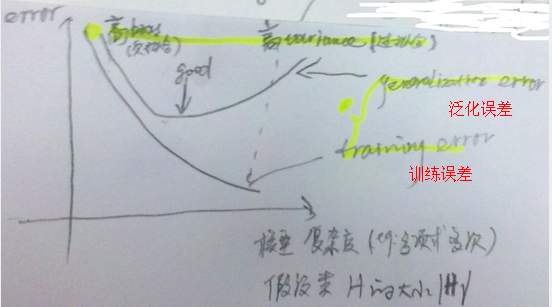
• $\epsilon$和$\hat{\epsilon}$关系：误差随着模型复杂度（VC维）的增加的变化趋势。模型复杂度过低：欠拟合；过大：过拟合。其中，模型复杂度为假设类$\left| H\right|$的大小，比如：某一个值为多项式多次。

  

• $H$：假设类。对于先行分类器：

• $D$： 某一种分布。

基本公式

1、
2、
3、

两个引理

1、联合界引理：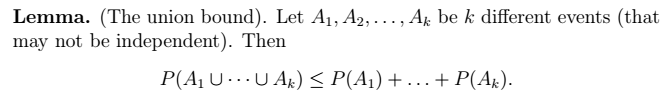

2、Hoeffding不等式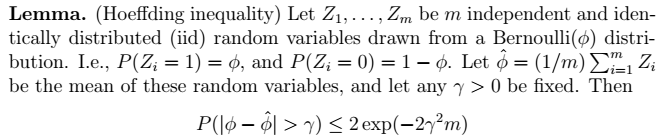

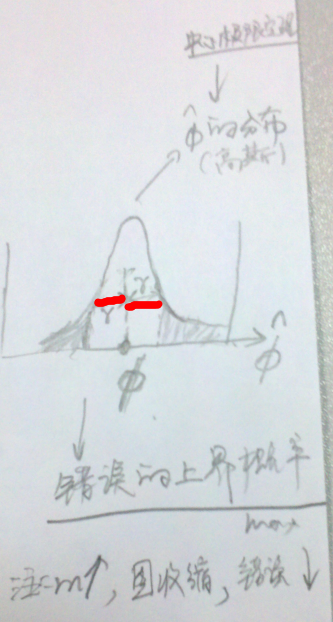
利用中心极限定理进行推导。其物理意义如下图所示。其中，表示阴影的概率，即错误的上届概率。当m增大时，钟形图收缩，误差下降。

$H$为有限的

即：
其中，H为：
1、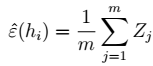
2、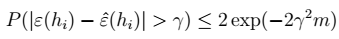
即：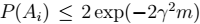

表示：

• $m$很大时，右边很小，两个误差很接近。
• 是人为给定的值。

3、对于任意h：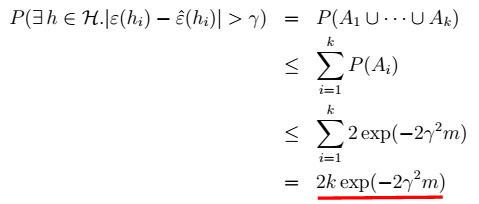

4、对于任意非h：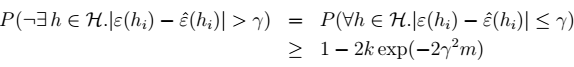

$m$很大时，右边很小，两个误差很接近。称为：一致收敛

5、我们关心的是m（样本大小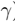）， （两个误差的差值）和概率（两个误差接近的概率）三者的值。下面，我们对其进行求解。
6、令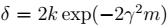，当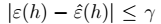时，我们得到样本的大小：

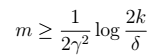
7、进一步，我们得到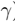的值：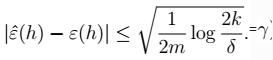

8、对7进行展开：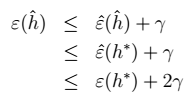

9、最终得到我们的定理：得到 $\gamma$ 的值

物理意义：我们可以近似地认为：为假设类H的偏差bias；为假设的方差variance。偏差表示误差的大小，随着模型复杂度增大而减小；方差表示拟合得有多好，随着模型复杂度增大，而先减小后增大。如下图：

10、最终，我们还得到另外一个定理，简而言之，固定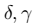，求m：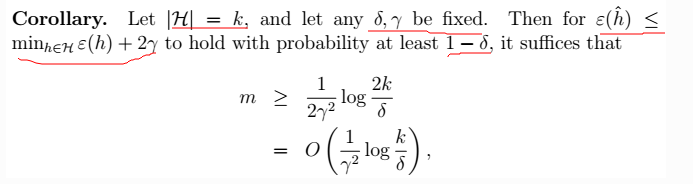

两个误差收敛的概率

下面开始为第10j

$H$为无限的—更实用

当H有无限值时，即：$|H|=\infty=k $。则上面公式10中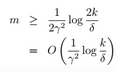，k将趋于无穷大；则m将无穷大。显然，这样是不行的。为了解决这种问题我们引入VC维。从而得到我们的理论。

shatters的定义

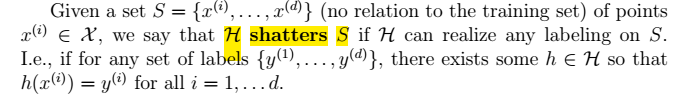
VC维的定义：

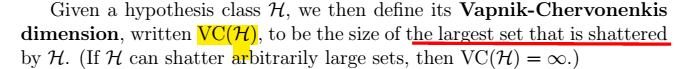
结论：对于n维线性分类器：$VC(H)=n+1$
eg. 时：$VC(H)=3$

最终我们得到学习理论中的重要理论：

1、定理：得到 $\gamma$ 的值

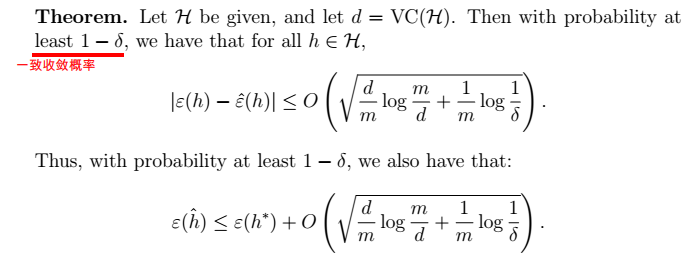
• m为样本数目；
• ，从而我们可以得到$\gamma$的值。

2、推论：得到$m$的值

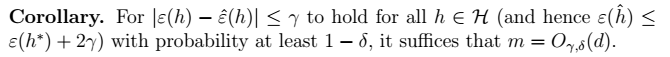
总结

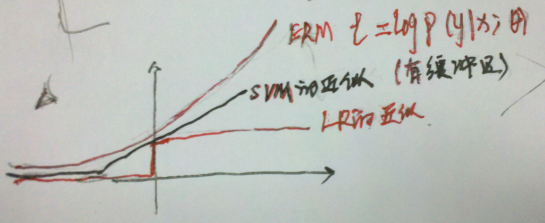
通过学习本节我们可以大概知道:SVM和LR都不是直接的ERM算法，都是对其近似。本章推荐的理论给出了这两种算法的直观含义的一种解释。如下图：