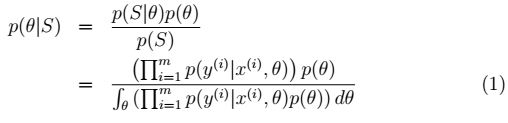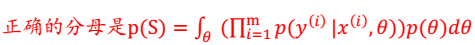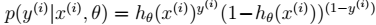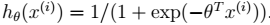机器学习11-1—贝叶斯统计和规则化

贝叶斯统计和规则化（ Bayesian statistics and regularization）

• 贝叶斯统计和规则化的目的：找更好的估计方法来减少过度拟合情况的发生。
• 回顾,总结：

  1. 线性回归中使用的估计方法是最小二乘法
  2. logistic 回归是条件概率的最大似然估计
  3. 朴素贝叶斯是联合概率的最大似然估计
  4. SVM 是二次规划。

频率学派和贝叶斯学派

看待 $\theta$ 的角度不同

频率学派（frequentist statistics）

认为θ不是随机变量，只是一个未知的常量，因此我们没有把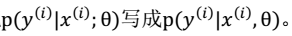

贝叶斯学派（Bayesian）

认为θ是随机变量。
步骤：
1、先验概率p(θ)：不同的θ值就有不同的概率。训练集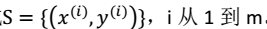：。则：θ的后验概率：

分母有误：

2、在θ是随机变量的情况下，如果新来一个样例特征为 x，那么为了预测 y。我们可以使用下面的公式：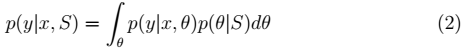

注：在不同的模型下计算方式不同。比如在贝叶斯 logistic 回归中：
其中，

3、进而得到期望：

　

4、注：

1. 这次求解p(y|x, S)与之前的方式不同，以前是先求θ，然后直接预测，这次是对所有可
   能的θ作积分。
2. 贝叶斯估计将θ视为随机变量，θ的值满足一定的分布，不是固定值，我们无法通过计算获得其值，只能在预测时计算积分。
3. 由于上述问题的存在；显然，后验概率p(θ|S)很难计算。为了解决这个问题，我们需要改变思路。看p(θ|S)公式中的分母，分母其实就是 P(S)，而我们就是要让P(S)在各种参数的影响下能够最大（这里只有参数θ） 。 因此我们只需求出随机变量θ中最可能的取值，这样求出θ后，可将θ视为固定值，那么预测时就不用积分了，而是直接像最大似然估计中求出θ后一样进行预测，这样就变成了点估计。这种方法称为MAP 最大后验概率估计（Maximum a posteriori）方法。

5、MAP 最大后验概率估计（Maximum a posteriori）方法，Θ估计公式为

6、进行预测：

$h{\hat{\theta}{MAP}}(X)=\hat{\theta}_{MAP}^{T}X$

7、总结与应用：

1. 与最大似然估计对比发现，MAP 只是将θ移进了条件概率中，并且多了一项p(θ)。
2. 一般情况下我们认为。
3. 贝叶斯最大后验概率估计相对于最大似然估计来说更容易克服过度拟合问题。原因：

   a. 整个公式由两项组成，极大化时，不代表此时p(θ)也能最大化。相反，θ是多值高斯分布，极大化时， p(θ)概率反而可能比较小。要达到最大化需要在两者之间达到平衡，也就靠近了偏差和方差线的交叉点。
   b. 这个跟机器翻译里的噪声信道模型比较类似，由两个概率决定比有一个概率决定更靠谱。作者声称利用贝叶斯 logistic 回归（使用θMAP的 logistic 回归）应用于文本分类时，即使特征个数 n 远远大于样例个数 m，也很有效。

L1和L2规则化？？？？？？？

老师上课没有讲到该部分，看了一下Pro Set3。也不是很理解。先引出正则化参数的损失函数，然后介绍了怎样最小化损失函数（过程不是很理解）。对于L1和L2在ODPS的XLab中有提到。后面，再仔细研究研究。对于L2：将后面一项改为2范数。

贝叶斯xi回归L1