• 本节：从逻辑回归引出支持向量机—>定义函数间隔和几何间隔—>最优间隔分类器（通过最大化间隔，得到最优）—>引出拉格朗日对偶（作用：通过对偶将算法变得更高效；处理高维）—>将对偶用到最优间隔分类器
• 本节都是针对很明显的分类’good’，如下图。

逻辑回归和支持向量机关系

两者关系

两者都可以实现分类。LR考虑全局（几经远离的点，通过调节中间线使其更远）；SVM考虑局部（不关心已经确定远离的点）。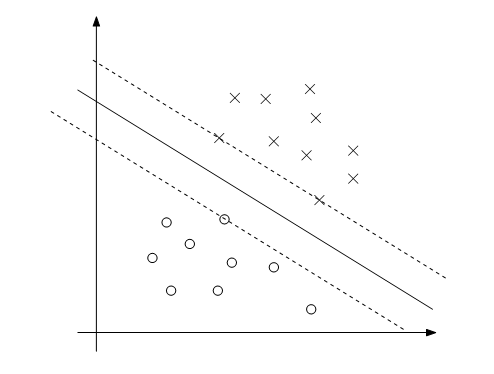

形式化表示LR—>SVM表示

$\theta$ 变为w和b。0、1变为0、-1。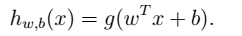

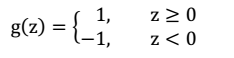
函数间隔和几何间隔

定义函数间隔—>通过归一化，再定义几何间隔—>两者关系。几何间隔的意义：点到超平面的距离。

• 函数间隔
  一个训练样本：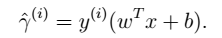
  所有训练样本：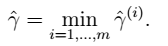
• 几何间隔
  一个训练样本：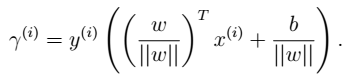
  所有训练样本：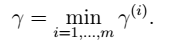
• 两者关系
  当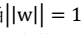时，两者等价。

最优化间隔分类器

几何间隔的优化（非凸规划：集合非凸集）—> 函数间隔的优化（非凸规划：最大化函数非凸函数）—> 改写后的规划（凸规划）

• 几何间隔的优化
  
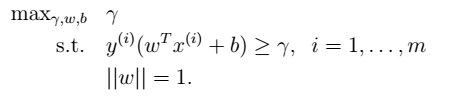
• 函数间隔的优化
  
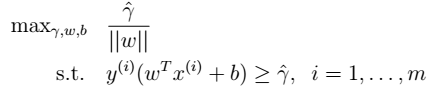
• 改写后的规划：令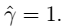，这样做的意义：将全局的函数间隔定义为1，即将离超平面最近的点的距离定义为，：
  

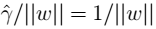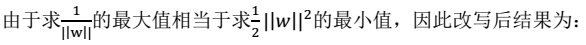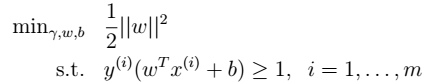
拉格朗日对偶

拉格朗日乘数法

• 1.最优化问题：
  
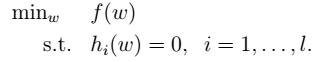
• 2.拉格朗日公式（拉格朗日算子）：
  
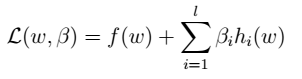
  其中，l为约束的个数（样本数目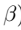），为拉格朗日乘数。
• 3.通过求偏导，解得参数
  

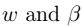
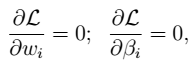
广义拉格朗日：拉格朗日+不等式

• 1.原始primal的最优化问题：
  
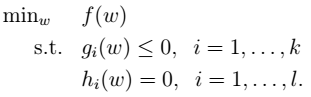
• 2.拉格朗日公式（拉格朗日算子）：
  
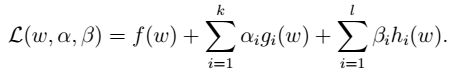
  其中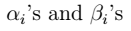，为拉格朗日乘数。
• 3.进一步得到
  
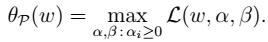
  即：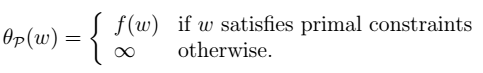
  
• 4.从而将问题转化（p:primal）：
  
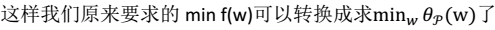
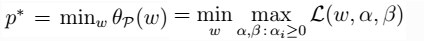
• 5.定义对偶问题（D:dual）：
  定义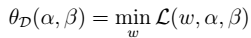：，则：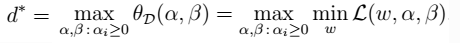
  
• 6.得到不等式关系：
  
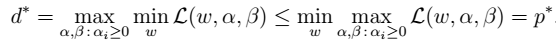
• 7.上面两者等价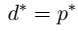的条件，KKT条件：
  
  ，即KKT条件：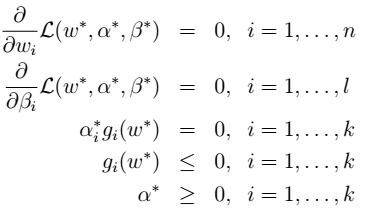
  

  注:

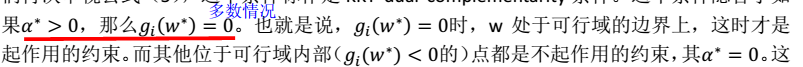
最优间隔分类器及拉格朗日对偶 在SVM中的应用

优化问题主要是求解w；b仅仅是一个参数。

SVM的优化问题

• 1、优化问题
  
  
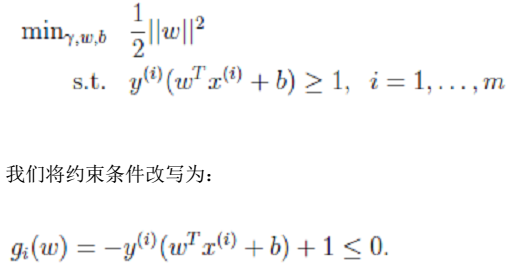
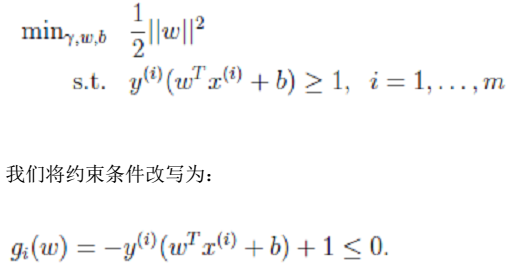
• 2、拉格朗日算子
  
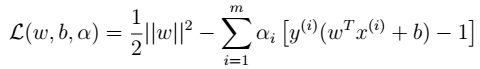
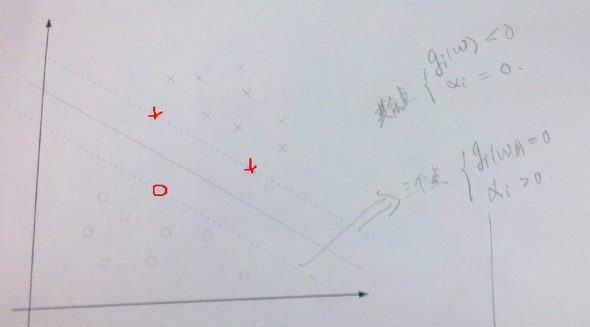
• 3、没有等式约束，只有不等式。下图中虚线上的三个点称为支持向量（支持向量机中的支持向量）。三点的函数间隔为1。。
  

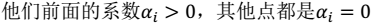  求解最优化问题

• 1、对偶问题
  
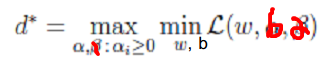
• 2、求解极小化问题：对w求偏导
  
  
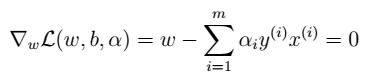
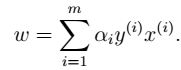
• 3、求解极小化问题：对w求偏导
  
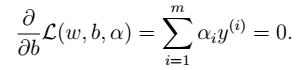
• 4、将w，b带入L中
  
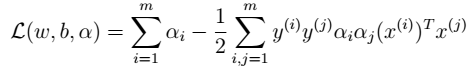
  注：该函数是关于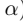的函数。通过极大化，来求解得到该值。然后，再得到w和b。
• 5、求解极大化问题：
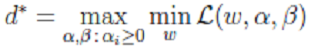
  凸规划：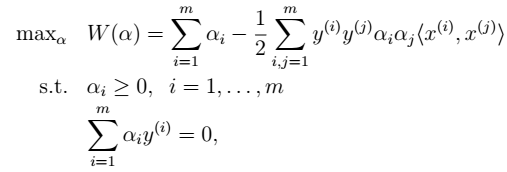
  
• 6、求解

  求解得到；
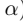  根据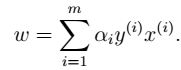得到w；
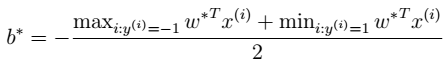  根据得到b。
  其中，b的意义：离超平面最近的正的函数间隔要等于离超平面最近的负的函数间隔。

• 7、进行预测
  如下公式所示:有了$\alpha_i$，我们不需要求出w，只需将新来的样本和训练数据中的所有样本做内积和即可。那有人会说，与前面所有的样本都做运算是不是太耗时了？其实不然，我们从KKT条件中得到，只有支持向量的$\alpha_i$> 0，其他情况$\alpha_i$= 0。