生成学习算法

说明：

• m为样本数目，i为第i个样本数目；
• joint likelihood ：联合似然估计

  判别学习算法和生成学习算法的区别：

算法	Learn	说明	概率类型
判别学习算法	$P(y/x)$	特征x下，输出y的概率	先验概率（经验为x）
生成学习算法	$P(x/y)和P(y)$	在模型y（为良性肿瘤）下，特征x发生的概率	后验概率（投‘果’探‘因’）——条件概率

第一个生成学习算法：GDA（高斯判别分析）

特点

• 假设输入x连续，服从多元高斯分布。
• 本例中y服从伯努利分布

GDA模型

• 输入x连续，服从多元高斯分布。
• y服从伯努利分布
  

似然函数

最大化似然函数得到所需参数

GDA与LR的区别

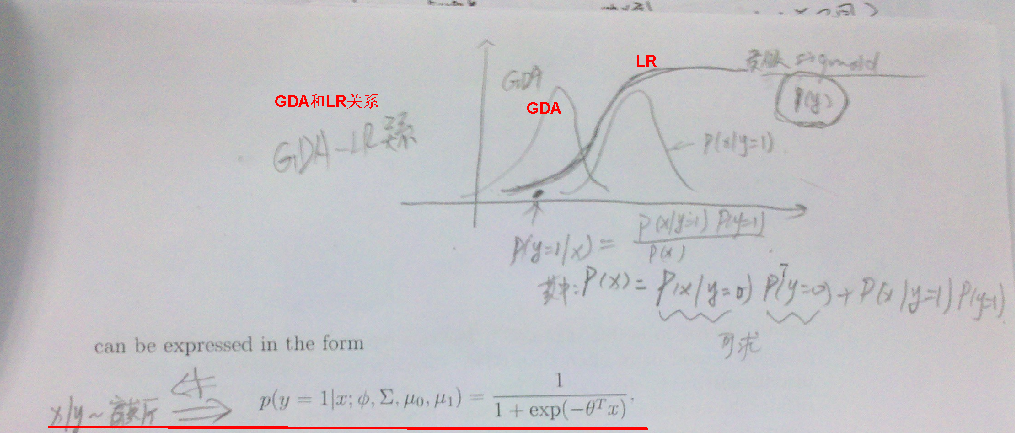
第二个生成学习算法：Navie Bayes朴素贝叶斯

特点

• 输入x离散，服从伯努利分布 （这也是为什么成为“朴素”的原因）。但是，x是多元伯努利事件模型。
• 本例中y服从伯努利分布

贝叶斯假设

输入变量x相互独立（在给定y的基础上）。

NB模型

• 模型—>最大化似然函数—>得到参数—>进行预测
• 模型及最大化
  
• 最大化似然函数得到的参数
  
• 进行预测
  

Laplace平滑法

用来处理，防止$0/0$的情况。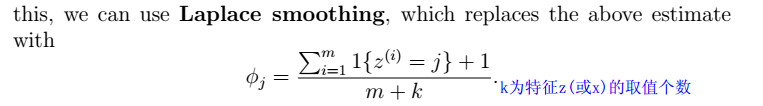

平滑后的NB参数：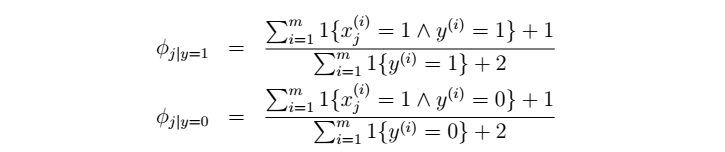

第三个生成学习算法：NB的第一种变形：多项式事件模型（处理文本）

• 生成模型
  
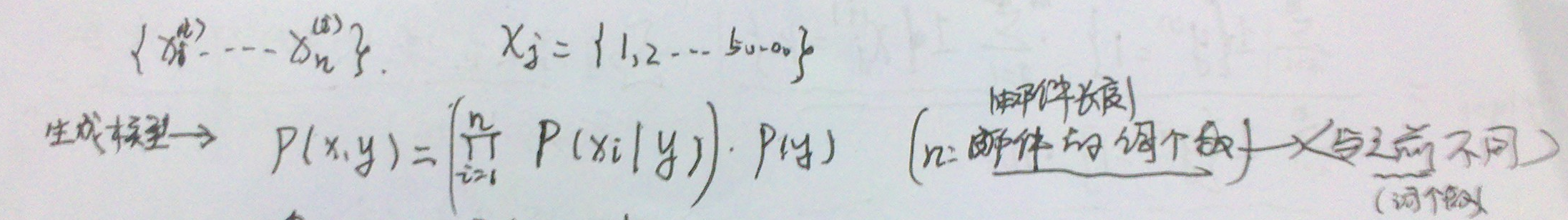
• 似然函数
  
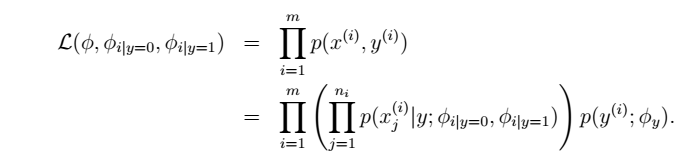
• 最大化似然函数得到参数
  
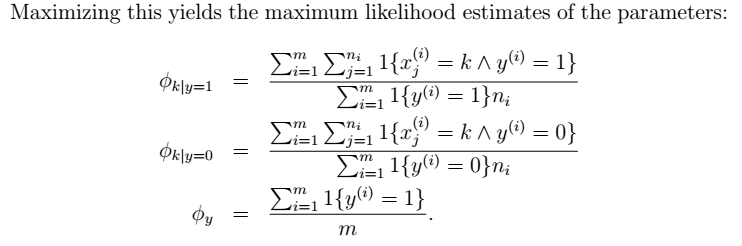
• 参数的物理意义
  
• Laplace平滑处理
  

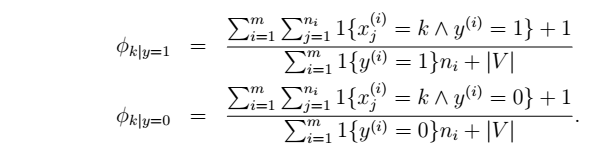
第四个生成学习算法：NB的第二2种变形：x可以取K个值

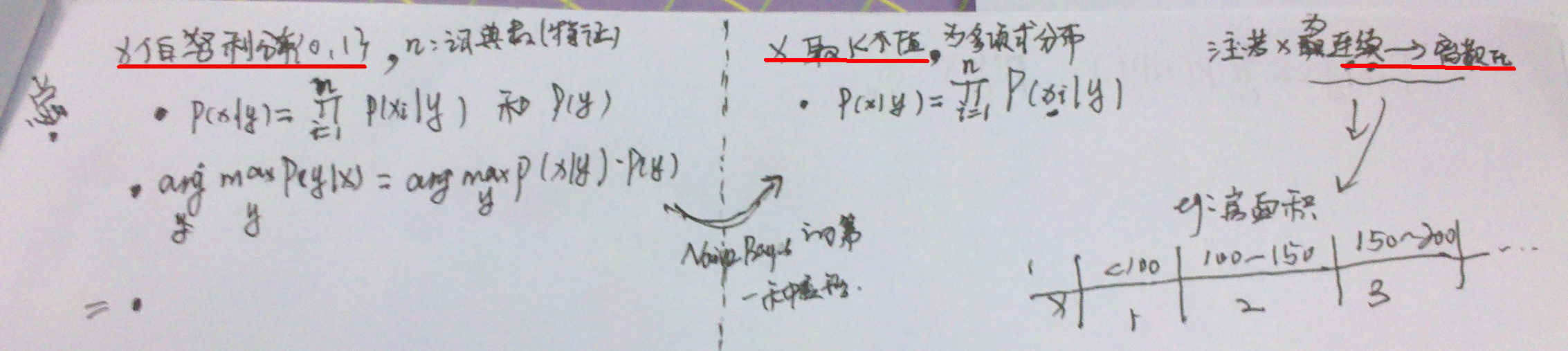
疑问

• 怎么样最大化似然函数，得到参数（似乎不是利用梯度法，或者牛顿法）？这个老师让自己去想。。。