机器学习2-GLM 广义线性模型

对于高斯分布、伯努利分布、多项式分布，均称之为GLM。

指数族

• 将高斯分布、伯努利分布、多项式分布转换为指数族，可以方便求解：首先，由$p（y|x;\theta）$ 得到$T(y),a(y),b(y)$； 然后，再经 $g(x)—>h(x)—>L(x)—>l(x)$(正则响应函数，学习算法的输出函数，似然函数，log似然函数)，得到结果。
  
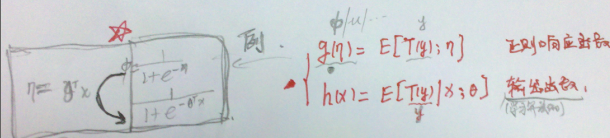
• 似然函数：表示某种事件发生的可能性；因此，一般似然函数表示为概率相乘的形式。$E(T(y)|x;\theta)$
• 指数族的三要素：$T(y),a(y),b(y)$

多分类逻辑回归（指数族在多项式分布中的应用）<—->LR的推广

二分类逻辑回归

多分类逻辑回归

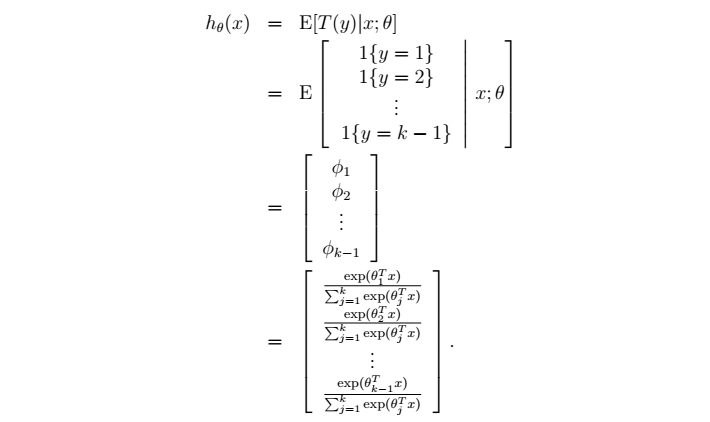
总结

GLM，以上两种方法，最终都得到似然函数，然后，利用梯度上升法或者牛顿法，进行求解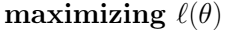
。

梯度上升法

。
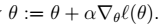例如：而分类逻辑回归：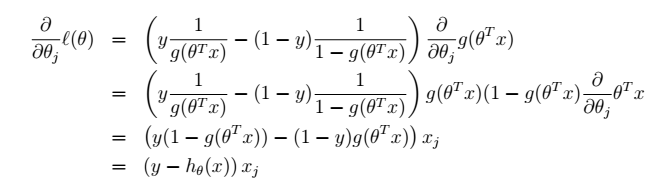

最终得到：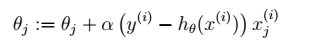

牛顿法

速度快，只需迭代十多次，但是，计算量很大。