一、 符号说明

$m$:样本数目（行数）<—>$i$某一行
$n:$特征数目（列数）<—>$j$某一列
$x,y$:输入和输出变量
$i^{th}$:training example<—>$(x^{(i)}, y{(j)})$
$\theta$学习参数
$h_{\theta}(x)$:输出函数

二、 算法总结

1. 最小均方（误差）算法LMS

该算法是为了使损失函数最小。损失函数为：


得到梯度下降的基本算法，下面会对其展开详细说明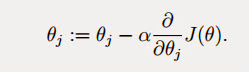

1.1 批量梯度下降

缺点：不适合数据量很大的情况

1.2 随机梯度下降

1.3 另外一种最小化$J_{\theta}$的算法最小二乘法

$(J=0)$

2. 局部加权线性回归

优点：在一定程度上防止了过拟合和欠拟合

• 参数化的学习算法：有固定参数学习，用来数据拟合
• 非参数学习算法： 局部加权线性回归
  

  3.逻辑回归（第一种：最大化$L(\theta)$）

• 基本公式：
  
• $\theta$的训练方法：利用梯度上升，来最大化似然函数(Likehood Function):
  
• 注：得到的最终结果，与LMS中的循环规则完全一样。但是，不同之处在于：此处$h_{\theta}(x^{(i)})$为非线性的。

4.牛顿（第二种：最大化$L(\theta)$）

三、 从概率角度解释最小化$J$的含义

使误差为0的概率最大<—>最大化相似函数$l(\theta)$或者$L(\theta)$<—>最小化$J$ ：最大似然估计

Written with StackEdit.